Problem set 7: Lists
This assignment is due on Wednesday, March 5 at 11:59pm. Submit it using Handin as assignment ps7. Corrections can be presented until Friday, April 4.
This problem set builds on the skills that we introduced in Lectures 2−9 and 11−14. To encourage you to review those lectures, your grade on this assignment will be capped by your grade on those lectures. You can resubmit lecture exercises at any time.
Remember to follow the design recipe whenever you design or write a function. In particular, every type mentioned in a signature must be introduced by a data definition, except for these well-known types: Number, Image, String, Color, Boolean, KeyEvent, MouseEvent, Posn, Anything, NaturalNumber, ListOfNumbers, 1String.

1 Representing ancestors
; An FT (short for family tree) is one of: ; - (make-no-parent) ; - (make-child FT FT String N String) (define-struct no-parent []) (define-struct child [father mother name date eyes])
Exercise 1. Who are you thinking of? You don’t need to have met this person or be in contact with them (so for example you can choose a celebrity). But they must be a real person (so for example you cannot choose Killmonger from Black Panther).
Hint: If you have trouble thinking of a real person, try yourself first: try to write down your own ancestors by giving an FT. Then, think of someone else you know and try to write down their ancestors by giving another FT.
Exercise 2. Who are this person’s ancestors? If you can answer this question just by giving an FT, then you have not found “a person whose ancestors cannot be represented as an FT”, and you should go back to the previous exercise and think of someone else. In particular, just because an ancestor is unknown doesn’t mean that they cannot be represented as an FT; the textbook discusses such a situation explicitly.
Exercise 3. Why do this person’s ancestors not fit the data definition in the textbook?
2 Counting words
Exercise 4. Warmup: Design a function remove-<=100 that takes a ListOfNumbers and removes every number less than or equal to 100. Hint: Follow the template.
Exercise 5. Develop a data and structure definition for storing a Frequency, which combines a String and a Number and represents that many uses of that string. Call the structure frequency with fields word and count.
Exercise 6. Develop a data definition ListOfStrings that uses cons and empty to hold arbitrarily many Strings. Also, develop a data definition ListOfFrequencies that uses cons and empty to hold arbitrarily many Frequencys.
(cons (make-frequency "hi" 5) (cons (make-frequency "hello" 4) (cons (make-frequency "bye" 2) empty)))
(cons (make-frequency "hi" 5) (cons (make-frequency "hello" 4) (cons (make-frequency "hi" 2) empty)))
Exercise 7. Design a function count-word that consumes a ListOfFrequencies and a String and adds 1 to the frequency count for that string, producing a new ListOfFrequencies. If there is no Frequency for that string, the resulting ListOfFrequencies should have a Frequency with that string and the number 1.
Exercise 8. Design a function count-all-words that takes a ListOfStrings and produces a ListOfFrequencies with the frequencies counted from the entire list of strings.
Exercise 9. Download the text of Hamlet into the same folder as your file where you are completing this assignment.
Then, create a list of words from the downloaded file. You should use the read-words function from the 2htdp/batch-io library.
; (define hamlet-frequencies ...)
Exercise 10. Design a function frequents that consumes a ListOfFrequencies and produces a ListOfFrequencies that contains only the Frequencys from the original list where the number is more than 100. Use this to compute all the words used more than 100 times in Hamlet. Include this list in your submission, as another comment. (Did you know about the “Comment Out with Semicolons” command under the “Racket” menu in DrRacket? It’s handy.)
3 Turtle graphics
Move forward by a distance of 50.
Turn left 90 degrees.
Move forward by a distance of 50.
Turn left 90 degrees.
Move forward by a distance of 50.
Turn left 90 degrees.
Move forward by a distance of 50.
; A Trip is one of: ; - empty ; - (cons Step Trip) ; A Step is one of: ; - (make-draw Number) ; - (make-turn Number) ; *Interpretation*: angle is how many degrees to turn left (counterclockwise) (define-struct draw [distance]) (define-struct turn [angle])
(define square-trip (list (make-draw 50) (make-turn 90) (make-draw 50) (make-turn 90) (make-draw 50) (make-turn 90) (make-draw 50))) (define z-trip (list (make-draw 80) (make-turn -135) (make-draw 120) (make-turn 135) (make-draw 80)))
3.1 Measuring trips
Exercise 11. Design a function step-length that computes the length of a Step. In other words, this function should compute how much ink is used by the given Step. Turning doesn’t draw anything, so the length of a turn is 0.
Exercise 12. Design a function trip-length that computes the length of a Trip. In other words, this function should compute how much ink is used by the given Trip. That is the total amount of ink used by all the Steps in the Trip. Hint: Follow the template for processing a Trip, so use step-length and trip-length.
3.2 Drawing trips
; A Turtle is (make-turtle Number Number Number) ; *Interpretation*: dir=0 faces east, ; dir=90 faces north, ; dir=180 faces west, ; dir=270 faces south (define-struct turtle [x y dir])
50 * sin(dir * pi / 180)
50 * cos(dir * pi / 180)
Exercise 14. Design a function draw-step that draws a given Step taken by a given Turtle on a given Image. Use the function scene+line provided by the 2htdp/image library in your examples and your definition; choose your favorite color. Also use the function move you just designed. Recall that turning doesn’t draw anything.
Exercise 15. Now design a function draw-trip that draws a given Trip taken by a given Turtle on a given Image. Use the functions move and draw-step you just designed.
Try draw-trip on example trips such as square-trip and z-trip.
3.3 Repeating trips
Exercise 16. Let’s make some pretty pictures. Design a function repeat that takes a NaturalNumber and a Trip and returns a new Trip that repeats the given Trip the given number of times. Hint: Follow the template for processing a NaturalNumber, and use append. This function actually works not just for trips but also for other lists.
(define hexagon-trip (repeat 6 (list (make-draw 50) (make-turn 60))))
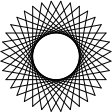 And this trip should look like a ring:
And this trip should look like a ring:
(define ring-trip (repeat 36 (list (make-draw 100) (make-turn 130))))
Help other students by answering this ungraded question: what did you have to learn to finish this problem set that we didn’t teach? Post your answer to Discord in the #ps7 channel, or put it as a comment at the bottom of your Handin submission.
4 Challenge
Some restaurants offer meal deals like this: the customer can choose one appetizer out of a list of appetizers, one main entrée out of a list of main entrées, and one dessert out of a list of desserts. That would make a 3-course meal, but some restaurants offer 2-course meals or 5-course meals.
(check-expect (deals (list (list "soup" "salad" "fries") (list "sandwich" "stir fry") (list "chocolate" "tofu" "affogato"))) (list (list "soup" "sandwich" "chocolate") (list "soup" "sandwich" "tofu") (list "soup" "sandwich" "affogato") (list "soup" "stir fry" "chocolate") (list "soup" "stir fry" "tofu") (list "soup" "stir fry" "affogato") (list "salad" "sandwich" "chocolate") (list "salad" "sandwich" "tofu") (list "salad" "sandwich" "affogato") (list "salad" "stir fry" "chocolate") (list "salad" "stir fry" "tofu") (list "salad" "stir fry" "affogato") (list "fries" "sandwich" "chocolate") (list "fries" "sandwich" "tofu") (list "fries" "sandwich" "affogato") (list "fries" "stir fry" "chocolate") (list "fries" "stir fry" "tofu") (list "fries" "stir fry" "affogato")))
