Problem set 12: Accumulators
This assignment is due on Wednesday, April 23 at 11:59pm. Submit it using Handin as assignment ps12. Corrections are not allowed.
This problem set builds on the skills that we introduced in Lectures 2−9, 11−19 and 26. To encourage you to review those lectures, your grade on this assignment will be capped by your grade on those lectures. You can resubmit lecture exercises at any time.
Remember to follow the design recipe whenever you design or write a function. In particular, every type mentioned in a signature must be introduced by a data definition, except for these well-known types: Number, Image, String, Color, Boolean, KeyEvent, MouseEvent, Posn, Anything, NaturalNumber, ListOfNumbers, 1String, [ListOf X], [NEListOf X]. When you write a function using an accumulator, you must provide an accumulator statement. An accumulator statement should explain what the accumulator is, not how to use or change the accumulator.
Generative recursion is not in this problem set, except in the challenge.
1 Accumulating while processing a natural number
; count : NaturalNumber -> [ListOf NaturalNumber] ; returns the given number of natural numbers in ascending order (define (count n) (count/a n 0)) (check-expect (count 0) empty) (check-expect (count 4) (list 0 1 2 3)) ; count/a : NaturalNumber NaturalNumber -> [ListOf NaturalNumber] ; returns the given number of natural numbers in ascending order ; *Accumulator*: next is the next number to produce (define (count/a n next) ???)
; numbered : NaturalNumber -> [ListOf String] ; returns the given number of strings like "0." "1." "2." (define (numbered n) (numbered/a n 0)) (check-expect (numbered 0) empty) (check-expect (numbered 4) (list "0." "1." "2." "3.")) ; numbered/a : NaturalNumber NaturalNumber -> [ListOf String] ; returns the given number of strings like "0." "1." "2." ; *Accumulator*: next is the next number to use (define (numbered/a n next) ???)
Exercise 3. Abstract from count (along with its helper count/a) and numbered (along with its helper numbered/a). Because we are abstracting from pairs of functions, there is no difference between how count calls count/a and how numbered calls numbered/a, just as there is no difference between how how count/a calls itself and how numbered/a calls itself. Call your new abstraction my-build-list (along with its helper my-build-list/a). As usual, these functions should have their own signature and purpose statements. Your new abstraction my-build-list should behave like the built-in function build-list, except the order of the two inputs can be different. Don’t forget to redefine count and numbered using my-build-list.
2 Accumulating while processing a list
Hint: all uses of accumulators in this section are context-preserving, meaning that the result of the recursive call is same as the result of the overall call.
; product : [ListOf Number] -> Number ; returns the product of the given numbers (define (product lon) ...) (check-expect (product empty) 1) (check-expect (product (list 10 20 30)) 6000) ; product/a : [ListOf Number] Number -> Number ; returns the product of the given numbers ; *Accumulator*: prod is the product of numbers seen so far (define (product/a lon prod) FILL-IN-THIS-BLANK)
Recall that zero times anything is zero. So, as soon as product/a encounters zero in the list, it can conclude that the result is zero. Implement this shortcut by adding a case to the cond in product/a.
Exercise 5. You own a small business in a foreign country, and you must pay taxes to the government according to the wages you pay to your employees. The payroll tax rate is 10%. Therefore, according to the tax laws of this country, before paying each dollar of wages to your employees, you must pay 10 cents of taxes to the government. Of course, you can pay taxes earlier than required, so for example, if you paid 20 cents of taxes yesterday, then you are allowed to pay $1 of wages today and another $1 of wages tomorrow. The general rule is that the total amount of taxes paid so far must be at least 10% of the total amount of wages paid so far.
; A Payment is one of: ; - (make-wage Number) ; - (make-tax Number) (define-struct wage [amount]) (define-struct tax [amount])
(check-expect (underpaid? (list (make-tax 0.1) (make-wage 1))) false) (check-expect (underpaid? (list (make-wage 1) (make-tax 0.1))) true) (check-expect (underpaid? (list (make-tax 0.2) (make-wage 1) (make-wage 1))) false) (check-expect (underpaid? (list (make-tax 0.1) (make-wage 1) (make-wage 1))) true)
Exercise 6. There is a robot in a room. The room is a square whose size is 20 feet by 20 feet. The location of the robot is represented by a Posn. The center of the room is (make-posn 0 0), so the X and Y coordinates of the robot are confined to between −10 and 10.
The robot obeys movement commands. A movement command is a Posn whose two fields say how much to try to add to the X and Y coordinates of the robot. For example, if the robot is at (make-posn 3 4) and tries to move by (make-posn 2 0), its location becomes (make-posn 5 4). However, if the robot tries to move outside the room, it stops at a wall. For example, if the robot is at (make-posn 9 4) and tries to move by (make-posn 2 0), its location becomes (make-posn 10 4), not (make-posn 11 4).
Design a function end-up that takes a list of movement commands and returns where the robot would end up if it starts at the center of the room and obeys the commands in the given order.
Exercise 7. A radio show is represented by the following information: the name of the show and the contents of the show. The contents are program segments and commercial ads, arranged in some order into a list. For each segment, we are given its name and its running time in minutes. For each ad, we are given its name, its running time in minutes, and the profit it generates in dollars.
Here are the data definitions that model a radio show:
; A Show is (make-show String [ListOf Content]) (define-struct show [name contents]) ; A Content is one of: ; - (make-segment String Number) ; - (make-ad String Number Number) (define-struct segment [name minutes]) (define-struct ad [name minutes profit]) ; Examples of data: (define life-segment (make-segment "Carriage" 10)) (define news-segment (make-segment "Consider" 12)) (define music-segment (make-segment "Concerto" 8)) (define site-ad (make-ad "Trka" 2 150)) (define game-ad (make-ad "Tron" 2 300)) (define car-ad (make-ad "Trabant" 1 500)) (define show1 (make-show "Serious" (list news-segment car-ad game-ad car-ad life-segment site-ad))) (define show2 (make-show "Fun" (list life-segment car-ad game-ad site-ad music-segment car-ad)))
(check-error (... ...) "/: division by zero")
You must use only one recursive function. This recursive (helper) function must follow the template for processing a [ListOf Content] (so it must not use make-show), and it must use two accumulators, which must be numbers.
Exercise 8. The show producer wants to make sure that the list of contents does not contain 5 or more minutes of contiguous ads without a segment. So, show1 is OK, but show2 is not acceptable, because the total duration of the ads car-ad game-ad site-ad is 5 minutes, which is too long.
Using the same data definitions as in the previous exercise, design a function ads-ok? that produces true if the given show is acceptable and produces false otherwise. Again, don’t use make-show.
3 Accumulating while processing a tree
; A BinaryTree is one of: ; - (make-leaf Number) ; - (make-node Number BinaryTree BinaryTree) (define-struct leaf [n]) (define-struct node [n first second]) (define bt1 (make-node 3 (make-leaf 4) (make-leaf 5))) (check-expect (bt-cumulative bt1) (make-node 3 (make-leaf 7) (make-leaf 8))) (define bt2 (make-node 100 bt1 (make-leaf 10))) (check-expect (bt-cumulative bt2) (make-node 100 (make-node 103 (make-leaf 107) (make-leaf 108)) (make-leaf 110)))
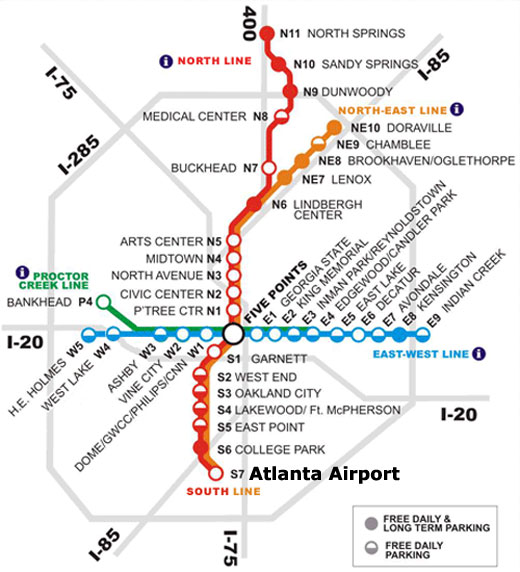
; A SubwayForest is a [ListOf SubwayTree] ; A SubwayTree is (make-tree Number String SubwayForest) (define-struct tree [distance station forest]) (define atlanta-five-points (list (make-tree 7 "Airport" empty) (make-tree 9 "Indian Creek" empty) (make-tree 6 "Lindbergh Center" (list (make-tree 5 "North Springs" empty) (make-tree 4 "Doraville" empty))) (make-tree 3 "Ashby" (list (make-tree 2 "H.E. Holmes" empty) (make-tree 1 "Bankhead" empty))))) (define lausanne-gare (list (make-tree 4 "Ouchy-Olympique" empty) (make-tree 1 "Lausanne-Flon" (list (make-tree 8 "Croisettes" empty) (make-tree 9 "EPFL" (list (make-tree 5 "Renens-Gare" empty))) (make-tree 15 "Echallens" (list (make-tree 5 "Bercher" empty)))))))
Design a function forest-cumulative that takes a SubwayForest as input and returns another SubwayForest. In the input, the distances are measured between each station and its parent, but in the output, the distances should be measured between each station and the root of the tree. For example, in atlanta-five-points above, the distance for North Springs should change from 5 to 11, because North Spring is 5 stops from Lindbergh Center but 11 stops from Five Points. In short, the input distances are relative and the output distances are absolute.
4 Challenge
; A Map is [ListOf Highway] ; A Highway is (make-highway String String PositiveNumber) (define-struct highway (start end dist)) ; interpretation: the dist of a highway is a number of miles
Here’s an example of a Map:
(define map1 (list (make-highway "Indy" "Bloomington" 50) (make-highway "Indy" "California" 2000) (make-highway "St Louis" "California" 1900) (make-highway "St Louis" "Indy" 190) (make-highway "Bloomington" "Indy" 50) (make-highway "Bloomington" "Evansville" 90) (make-highway "Evansville" "St Louis" 150)))
Design a function distance that takes a Map and two strings (a starting point and a destination), and returns either the minimum total distance to go from the given starting point to the given destination using the given highways, or "no way" if there is no way.