Lab 11: Forking turtles
Use the “Intermediate Student with lambda” language on this and further assignments in this course.
In Problem set 7: Lists, you drew pictures by telling a turtle carrying a pen to move and turn. In this lab, you’ll expand the variety of pictures by allowing the turtle to clone itself.
Start by retrieving your past work. Or, you can start by downloading this sample solution. Don’t use “Save Page As” or “Save As”; use “Save Link As” or “Download Linked File” in your Web browser. If you can’t find the command, try right-clicking or two-finger-tapping or long-pressing.
1 Making branching trips
Move forward by a distance of 50.
- Give birth to a child turtle that follows these instructions:
Turn left 30 degrees.
Move forward by a distance of 50.
Turn right 30 degrees. In other words, turn left −30 degrees.
Move forward by a distance of 50.
; A Step is one of: ; - (make-draw Number) ; - (make-turn Number) ; - (make-fork Trip) ; *Interpretation*: angle is how many degrees to turn left (counterclockwise) (define-struct draw [distance]) (define-struct turn [angle]) (define-struct fork [child])
(define child-trip (list (make-turn 30) (make-draw 50))) (define y-trip (list (make-draw 50) (make-fork child-trip) (make-turn -30) (make-draw 50)))
Exercise 1. Define two more examples of Trips that use make-fork. Call them fork-trip1 and fork-trip2.
Exercise 2. Write the template process-trip for a function that processes a Trip, and the template process-step for a function that processes a Step.
Exercise 3. Point out where the revised data definition for Step refers to the data definition for Trip. Does your template process-step refer to your template process-trip in the corresponding place? It should.
2 Measuring branching trips
Exercise 4. Update your design of the step-length function to allow an input Step that is a fork. Don’t change the signature, but remember to add the necessary examples: the length of (make-fork child-trip) is 50. Remember to follow the template for processing a Step, so your new definition of step-length should call trip-length.
Exercise 5. Add tests for trip-length using y-trip, fork-trip1, and fork-trip2. They should pass, even though you haven’t changed trip-length. Why?
3 Drawing branching trips
Exercise 6. Update your design of the move function, again to allow an input Step that is a fork. Again, don’t change the signature, but remember to add the necessary examples: giving birth to a child turtle does not move the parent turtle.
Exercise 7. Update your design of the draw-step function, again to allow an input Step that is a fork. Again, don’t change the signature, but remember to add the necessary examples. Follow the new template for processing a Step, so your new definition of draw-step should call draw-trip.
Exercise 8. Add a test for draw-trip that uses make-fork. It should pass, even though you haven’t changed draw-trip. Why?
4 Repeating branching trips
Exercise 9. Let’s make some more pretty pictures. Design a function radiate that takes a count (a NaturalNumber), an angle (a Number), and a Trip, and returns a new Trip. The new Trip should generate the given count of child turtles, and they should all start at the same current location and perform the same given trip, but after each child turtle should be a rotation by the given angle.
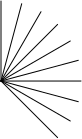For example, the fan to the right is made like this:
(check-expect (radiate 10 -15 (list (make-draw 80))) (list (make-fork (list (make-draw 80))) (make-turn -15) (make-fork (list (make-draw 80))) (make-turn -15) (make-fork (list (make-draw 80))) (make-turn -15) (make-fork (list (make-draw 80))) (make-turn -15) (make-fork (list (make-draw 80))) (make-turn -15) (make-fork (list (make-draw 80))) (make-turn -15) (make-fork (list (make-draw 80))) (make-turn -15) (make-fork (list (make-draw 80))) (make-turn -15) (make-fork (list (make-draw 80))) (make-turn -15) (make-fork (list (make-draw 80))) (make-turn -15)))
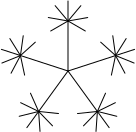And the flower to the right is made like this:
(radiate 5 -72 (append (list (make-draw 50) (make-turn 120)) (radiate 7 -40 (list (make-draw 20)))))
(check-expect (enlarge-trip 2 y-trip) (list (make-draw 100) (make-fork (list (make-turn 30) (make-draw 100))) (make-turn -30) (make-draw 100)))
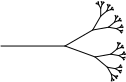Exercise 11.
The leafy tree to the right is generated by the following function.
; generations : NaturalNumber -> Trip ; produce a turtle family ; of that-many generations
(check-expect (generations 0) empty) (check-expect (generations 1) (list (make-draw 64) (make-turn 30) (make-fork empty) (make-turn -50) (make-fork empty))) (check-expect (generations 2) (list (make-draw 64) (make-turn 30) (make-fork (list (make-draw 32) (make-turn 30) (make-fork empty) (make-turn -50) (make-fork empty))) (make-turn -50) (make-fork (list (make-draw 32) (make-turn 30) (make-fork empty) (make-turn -50) (make-fork empty))))) (define (generations n) (cond [(= n 0) empty] [else (list (make-draw 64) (make-turn 30) (make-fork (enlarge-trip .5 (generations (- n 1)))) (make-turn -50) (make-fork (enlarge-trip .5 (generations (- n 1)))))]))
5 Challenge
Now that we’re able to produce images of Trips that turtles have taken, wouldn’t it be nice to watch as the turtles take these trips? Our goal in this challenge is to design a big-bang program which takes as input a Trip and animates the corresponding drawing.
Consider this problem before we allowed the turtle to fork. If there’s only one turtle, we might think of splitting a Trip into a past and a future; and having big-bang draw the past while over time shifting the future into the past.
Forking complicates this simple dynamic. One way forward is to view a Trip as a tree: a non-fork Step corresponds to extending a given branch, whereas a fork corresponds to a branch splitting into two. Given a Step in the tree, we measure its distance to the root of the tree by counting the number of non-fork Steps we took before it. Forks do not count. For example, in y-trip, the distance from (make-turn 30) to the root is one.
Design a function truncate which takes a NaturalNumber and a Trip and returns as much of the given Trip as possible so long as every Step in the resulting Trip has distance to the root strictly less than the given number. Here are example truncations of y-trip:
(check-expect (truncate 0 y-trip) empty) (check-expect (truncate 1 y-trip) (list (make-draw 50))) (check-expect (truncate 2 y-trip) (list (make-draw 50) (make-fork (list (make-turn 30))) (make-turn -30))) (check-expect (truncate 3 y-trip) y-trip)
Next, using truncate, design a big bang program which displays successively more generous truncations:
