|
High-level programming languages for symbolic processing have been widely studied since the inception of Lisp in the late 1950's. The family of symbolic languages is now a diverse group, encompassing Lisp and its derivatives, purely functional languages like Haskell, logic programming (e.g. Prolog), Smalltalk, and many more. One of the attractive properties of these languages is that they unburden the programmer from storage management considerations such as allocation and reclamation of objects. By automating these low-level implementation details, programs written in these languages are rapidly developed and are usually simpler to understand and maintain.
Interest in symbolic processing has further increased in recent years as parallel computers have made inroads into the mainstream computer market. Small- to medium-sized RISC-based shared memory MIMD architectures will characterize the servers and workstations of the next decade. Symbolic languages are good candidates for programming these machines; their heap-orientation maps well to the shared memory architecture and their underlying computational models often facilitate parallelism. As with storage management, symbolic languages can subsume low-level concurrent programming details such as process creation, communication, synchronization, load balancing, scheduling and data distribution; detail that seriously complicates programs written in traditional imperative languages. Symbolic languages remove much of this ``noise'' from programs, improving readability, portability, and scalability of the code. Additional benefits are reduced software development cycles and maintenance costs. Removing these details from the language shifts the burden of memory and process management from the programmer to the language implementation. The incorporation of these difficult problems into the language implementation domain is a topic of active research.
The subject of this dissertation is the design and implementation of DSI; a virtual machine and microkernel for list-based, symbolic multiprocessing. I also describe and briefly analyze the operation of Daisy, an applicative language built on top of DSI. DSI and Daisy are designed around suspending construction, a Lisp-derived, demand-driven, parallel computation model developed at Indiana University. This dissertation provides insights into the problems, issues and solutions involved in a real parallel implementation of a language based on suspending construction. Previous incarnations of DSI/Daisy have been multi-threaded sequential implementations, designed primarily to explore the demand-driven, lazy aspect of suspending construction-based computation. The premise of suspending construction as a parallel processing vehicle, while much discussed, was not realized in an actual implementation. This dissertation work extends DSI's virtual machine architecture to handle the complexities of a shared-memory, MIMD parallel implementation. The DSI kernel, an embedded operating system that handles resource management for programs running on this architecture, is redesigned from the ground up to handle parallel task, memory and device management in parallel, using a loosely-coupled, distributed design. The algorithms presented here are based on an implementation of DSI/Daisy on the BBN Butterfly, a commercial multiprocessor.
In a practical sense, this work results in a platform for further exploration of parallel and system-level computing based on suspending construction, with a richer development environment and improved language, interfaces and tools. In a broader sense, the contributions herein can be categorized into three main areas. First, the virtual machine description highlights the key hardware needs of suspending construction and how that differentiates DSI's machine design from conventional architecture. This suggests specific enhancements to stock hardware that would greatly benefit execution of languages oriented toward fine-grained list processing. Secondly, we present the design of a low-level, general kernel for fine-grained parallel symbolic processing based on this architecture. The kernel is described in terms of memory, process and device management algorithms. My approaches to these problems suggest new, alternative strategies for resource management in parallel symbolic languages of all flavors. Finally, a discussion of suspending construction in the context of the Daisy language highlights the effectiveness and limitations of this computing model for parallel processing, and suggests ways in which the latent parallelism of the model might be better exploited in future designs of the language.
The topics discussed in this thesis are a cross-section of the areas of programming languages, computer architecture and parallel processing. As such, this dissertation will primarily be of interest to language implementors and, to a lesser degree, other researchers in the aforementioned areas. In particular, much of this work is applicable to other parallel symbolic language implementations, especially applicative languages.
Chapter 2 provides general background and introduction to the topics and issues discussed in the rest of the thesis, particularly resource management problems for dynamic, fine-grained parallelism. Chapter 3 discusses the design of DSI's virtual machine. Chapter 4 describes the overall structure of DSI's kernel, which provides background for references to relevant implementation details in the following chapters. Chapters 5-7 present the design and implementation of the kernel's resource management algorithms along memory, process and device categories.
Chapter 8 discusses aspects of suspending construction in the Daisy language. The language itself is only tangentially relevant to this thesis as a vehicle for expressing suspending construction programs, and a brief introduction to the language and its primitives are all that is required. A more thorough introduction and tutorial to the Daisy language is the Daisy Programming Manual [Joh89b] and associated research papers (see bibliography).
Chapter 9 summarizes the work accomplished, indicates directions for future research and references related work in Lisp-based parallel symbolic processing (comparisons are sprinkled throughout the thesis).
Halstead [RHH85] notes that numerical computation generally has a relatively data-independent flow of control compared to symbolic computation. Compiler dependence analysis can turn this data independence into a fair degree of parallelism that is amenable to vector, pipelined and SIMD approaches. The parallelism of symbolic computation, on the other hand, can be very data-dependent; this suggests a MIMD approach in which parallelism is primarily generated and controlled dynamically. Although parallel symbolic languages are quite diverse and may differ substantially in many ways, they all share a core set of resource management problems associated with this dynamic control of parallelism: task scheduling and load balancing, dynamic memory management, etc. Chapter 2 provides an introduction to many of these problems from a Lisp perspective.
The number of parallel symbolic language implementations has grown considerably in the last ten years or so. Most of these languages fall into one of the following broad categories:
The basis of suspending construction is a transparent decoupling of
structure formation from determination of its content in a symbolic
domain of lists and atoms.
Under most Lisp variants, structure is built recursively by
applicative-order evaluation of subexpressions, whose results form the
template for initializing the structure (usually a list).
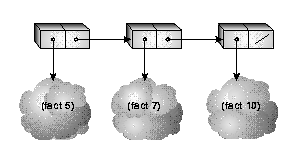
For example, evaluating the Lisp expression
where fact is the factorial function,
preforms three subexpression evaluations of (fact 5),
(fact 7) and (fact 10) before cons-ing
the results into a list.
Under suspending construction, suspensions are created in lieu
of subexpression evaluation, and a structure is returned containing
references to the suspensions.
A suspension is an independent, fine-grained, suspended process that contains any information necessary to compute the subexpression it represents. Normally a suspension remains dormant until an attempt is made to access it from a structure (a probe), which causes a kernel trap. At that point the system intervenes, activating the target suspension and temporarily blocking the probing process (which itself is a suspension). Once activated, a suspension attempts to compute its subexpression and replace its own reference in the structure with that of the result. When a suspension has converged in this manner, subsequent accesses (probes) to the same location fetch the expected manifest object. This cycle of probing--activation--convergence is known as coercing a suspension, and it is entirely transparent to programs, which are simply creating and manipulating data structures as usual. The system is responsible for detecting and scheduling suspensions as necessary.
We visualize suspensions as clouds;
figure 1 shows the result of a suspending version
of list construction applied to the previous example.
Between activation and convergence
a suspension will usually traverse some portion of its inputs,
coercing any existing suspensions that it happens to probe,
and it will also create its own data structures,
forming new suspensions as a byproduct.
Thus, a running program creates a
dynamic web in the heap of many thousands of suspensions all linked
together through data structures, as shown in figure
3.
 (Click on the image to see a larger 981x756 (138Kb) image)
(Click on the image to see a larger 981x756 (138Kb) image)
|
Thus, suspending construction provides a simple but complete automation of the important details of parallel programming: process decomposition, communication, and synchronization. Just as with automated storage management in Lisp programs, the programmer is not required to handle any of the complicated aspects of parallel task management and can concentrate on writing a suitably parallel algorithm. This leaves the ``hard details'' of parallel process management to the implementation, which is what this thesis describes.
To see this, consider two scheduling policies at the extreme ends of the scale:
The eager vs. demand-driven scheduling policies referred to above can really be viewed as two endpoints of a continuum [AG94, p.267], [Liv88]. By itself, demand-driven scheduling provides maximum laziness, computing no more than is absolutely necessary, but forgoes some opportunities for parallelism. Eager scheduling can generate too much parallelism. The ideal situation seems to lie somewhere between the endpoints of this scheduling continuum, and a number of ideas have been published in this area. Some of these, notably data flow reduction, start from an eager perspective and attempt to reduce parallelism. Lenient evaluation [Tra91] tries to take the middle ground, forgoing laziness but still attempting to achieve non-strict semantics where possible, making some sacrifices in expressiveness as a result. Still others, like DSI's approach, start from the demand-driven (lazy) perspective and relax it to allow safe eager parallelism and constrained speculative parallelism.
To extract implicit parallelism, an imperative language can employ dependence analysis and other compiler analytic techniques; this approach is popular for many ``dusty-deck'' Fortran applications, as well as for imperative symbolic programs [Lar91]. These methods are not always effective, however, primarily due to the increased number of dependences involved, as well as aliasing and other artifacts of imperative programming [AG94].
One alternative to these analytic techniques is to provide a history roll-back mechanism to be able to roll back the computation when conflicts occur due to side effects. At least one implementation of the Scheme language is based on this technique [TK88].
All of these techniques impose complications in various ways, either on the programmer to explicitly synchronize his program, on the compiler for analysis, or on the run-time system to roll back computation. Alternatively, a language can restrict or eliminate side-effects and not suffer these complications; such is the approach of the declarative family of languages, which includes ``pure'' functional languages, and also certain quasi-functional languages, like Daisy.
Daisy does not have side-effects in the traditional sense (it does provide top-level assignment of global function identifiers). There are two main reasons for this: laziness and implicit parallelism. Suspending construction does not preclude the use of side-effects, but their inclusion in the surface language would make it extremely difficult to reason about programs because demand-driven scheduling results in non-intuitive evaluation orders. A lack of side-effects also allows Daisy to take advantage of implicit parallelism opportunities. Removing side-effects removes all dependences from the program with the exception of flow dependences [AG94], which are handled by the probe/coercion mechanism described earlier. This makes suspensions mutually independent, and allows the system considerable flexibility in scheduling them. The consequences of this flexibility are particularly important for parallelism; suspensions can execute in any order, including lazily or concurrently, without affecting the result. This effectively reduces scheduling from a problem of efficiency and correctness and to one of efficiency only. That problem is determining which subset of suspensions to execute at a given time to achieve maximum system throughput, while minimizing the overhead of communicating scheduling information between processors. We want to avoid scheduling suspensions that are simply blocked awaiting the convergence of other suspensions.
Although Daisy lacks explicit side-effects, it is not
referentially transparent, a property shared by many
declarative languages.
Many computing problems arise that are inherently nondeterministic,
especially in the realm of systems programming.
Daisy addresses these problems by providing an applicative
nondeterministic construct.
's set primitive returns a copy of its list argument,
the copy permuted in an order determined by the convergence of the
suspensions in the argument list.
For example, the following Daisy expression
would likely return
The order reflects the cost of computing the three subexpressions.
The set primitive can be used to implement fair merge,
for expressing explicit speculative computation and concurrency,
and many asynchronous applications.
The rationale for including side-effects in parallel symbolic languages is elegantly laid out by Halstead in [RHH85], who appeals to arguments of expressiveness and efficiency. However, this approach negates many implicit opportunities for laziness or parallelism and leaves the problem of creating and synchronizing parallel processes in the programmer's domain. In this research we adopt the view that these details should be left to the underlying implementation as much as possible. Our concern is not with the expression of parallelism or concurrency in the language (see below), but rather with the inherent limitations on parallelism imposed by side-effects.
In regard to efficiency, a language with automated process management is unlikely to be as efficient as a more traditional imperative language such as Scheme or C. Just as there is a cost associated with doing automated storage management under Lisp (as opposed to explicit storage management under, say, C), there is a cost added with automating process management. The ever-increasing speed and capacity of hardware and gradual improvements in language implementation technology make this trade-off worthwhile in most situations.
The property of laziness can be considered as much a factor in language expressiveness as the inclusion of side-effects. Daisy's lack of side effects is a pragmatic approach to achieving laziness and parallelism rather than a means of upholding language purity. Similarly, the inclusion of indeterministic operators is a practical means to offsetting the constraints imposed by our choice to abandon side effects. Thus, we deemphasize equational reasoning in favor of expressiveness. This philosophy may help explain Daisy's seemingly odd position ``straddling the fence'' between imperative and pure functional languages.
Note that these distinctions are not always clear-cut; in actuality languages may overlap one or more of these areas. For example, Scheme with futures [RHH85] falls into the last category, but overlaps the second somewhat, since futures are not strictly semantically required to be parallel and thus may be optimized in certain ways [Moh90]1.2. This is similar to the notion of para-functional programming [HS86,Hud86]; the idea that programmers annotate programs to provide clues for the system without actually changing the semantics of the program or getting involved in resource management issues (although the latter approach is also a possibility [Bur84]). This is a step backward from complete automated parallelism, but still does not cross the line into explicit parallel decomposition of tasks or synchronization for side-effects, etc. Daisy straddles the second and third categories, for reasons which are explained in chapter 8.
The cost of suspending construction for a given expression can be analyzed as follows:
To avoid it, we could revert to strict evaluation in cases where neither concurrency nor laziness is possible or desirable. Strictness analysis [Hal87,HW87] can reveal instances in a program where evaluation could be safely strict, but doing so may forgo opportunities for parallelism. Determining whether or not to evaluate an expression in parallel depends on the cost of the computation as well as dynamic factors such as the input data and current system load. All in all, determining when not to suspend is a difficult problem. Daisy manages some suspension avoidance by unrolling evaluation code to test for trivial cases before suspending them, allowing programming annotations for strictness, and under compilation, using strictness analysis [Hal87,HW87].
A more ``brute force'' approach to efficiency is to optimize suspension handling to make it more competitive with strict evaluation; more progress has been made at the DSI level in this regard. There are three main areas targeted for optimization:
Friedman and Wise demonstrated that a pure applicative-order Lisp interpreter built using a suspending cons and suspension-aware versions of car and cdr has call-by-need semantics, resulting from suspended environment construction. They went on to describe how Landin's streams are naturally subsumed into such a system and how conditionals and other special forms can be implemented as simple functions due to the non-strict evaluation of function arguments [FW78e]. These revelations led to further observations on the ability to manipulate large or infinite data structures in constant space [FW78e].
Suspending construction naturally leads to output- or demand-driven computation [FW76c], because structure is coerced by an in-order traversal of the top-level data structures by the printer or other output devices. Printing a structure (and in the process, traversing it) propagates demand through suspension coercion to the fringe of the computation tree; in short, the output devices are the ultimate source of demand that drive the system.
In short order the connection was drawn between suspensions and multiprogramming [FW76b]. Since suspensions are mutually independent, self-contained objects, they can be coerced in parallel without mutual interference or synchronization. The problem is determining how to express parallelism in a demand-driven environment, which is naturally non-parallel. A few inherently parallel applicative constructs were developed, including functional combination [FW77,FW78c], a form of collateral function application; and multisets [FW78a,FW78b,FW79,FW81,FW80b], a nondeterminate form of list constructor which was the precursor to Daisy's current set construct.
These successive discoveries led to iterative refinements of the underlying suspending construction model, including the evolution of suspensions from simple thunks to processes and various proposals for architectural enhancements to support suspending construction on multiprocessors [FW78d,FW80a,Wis85a]. Much of the credit for this is due to Johnson [Joh81,Joh85,Joh89c,Joh89a,Joh89b] who was the primary developer on the early Daisy implementations.
The motivation behind the Daisy/DSI project is to explore systems-level and parallel programming from an applicative perspective. The division into the Daisy and DSI components allows us to study facets of this research at both a high and low level of implementation. Several sequential implementations of Daisy (and later, DSI) were developed, combining various aspects of this research. Each release has provided increasing levels of performance and features. The underlying list processing engine, dubbed DSI [Joh77,JK81], has undergone four major revisions. The surface language implemented on DSI is Daisy [Koh81,Joh89b], a pure language internally similar to Scheme, that is the high-level vehicle for exploring various ideas borne out of this research.
Daisy has been actively used for hardware- and systems-level modeling [Joh83,Joh84b,Joh84a,Joh86,JBB87,JB88,O'D87], applicative debugging [O'D85,OH87,O'D] matrix algebra [Wis84b,Wis84a,Wis85b,Wis86a,Wis86b,Wis87,WF87] and experimental parallel applicative programming.