|
screen: scnos: prsos: evlst: prsis: scnis: console: "&"
Application is denoted by infix colon (:), and associates to
the right.
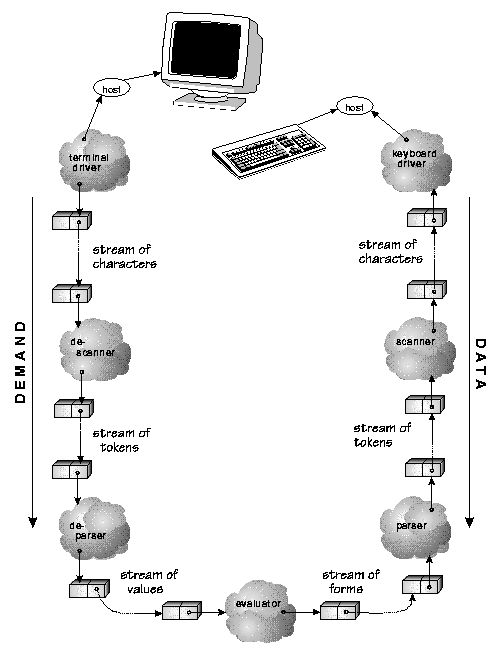
This program builds a stream pipeline as shown in figure
25.
Demand emanating from the printer (screen) ripples down through the pipeline to the input device, and data flows in the opposite direction. In the middle (evlst), programs are evaluated. Programs will typically create their own network of streams, which plug in transparently to this top-level stream pipeline. The demand rippling down through the output pipeline is what drives program computation.
quick = \L.
let:[[X ! Xs] L
if:[nil?:L L
nil?:Xs L
let:[[lo hi] partition:[X Xs]
append:[quick:lo [X ! quick:hi]]
]
]]
partition = \[p L]. part:[p L [] []]
part = \[p L lo hi].
let:[[X ! Xs] L
if:[nil?:L [lo hi]
le?:[X p] part:[p Xs [X ! lo] hi]
part:[p Xs lo [X ! hi]]
]]
append = \[L1 L2].
let:[[X ! Xs] L
if:[nil?:L1 L2
[X ! append:[Xs L2]] ]
]
|
Consider the application of quick to a list of numbers.
The result of quick:[...] eventually reduces to a sequence of
nested, suspended appends. This can be visualized as:
(this represents what a string reduction model might actually do).
Under normal output-driven evaluation, the printer, attempting to
coerce the head of this structure, causes the inner
suspended appends to unfold until the innermost append performs
a suspending cons (line 21 of figure 26).
This satisfies the demand of the next outer append
for X, so it also performs a lazy cons and converges.
In this manner, computation ripples back up to the topmost
append as the dependence chain is satisfied.
The printer then issues the first number of the result and
iterates, probing the second element, which repeats the entire
scenario just described.
There are two problems with this behavior. First, append is lazy in its second argument, which means the suspended recursive call quick:hi will not be coerced until the printer has output the entire result of quick:lo. Thus, no parallelism has been achieved. Secondly, the lazy cons occurring on line 21 results in N complete traversals of the suspended computation graph for outputting N total elements. Ideally, if we know that the entire structure is needed, we would like to propagate exhaustive demand [OK92], so that when demand ripples down through the inner appends, their result is completely coerced before converging. This would result in a single traversal of the computation graph, resulting in much less context switching. Neither of these problems are due to the kernel's default process management. Given a scheduling request, the kernel will execute that suspension and any suspensions that it coerces until such time as it converges. Rather, there are two problems are at the language level which are responsible:
Suppose we were to address the first problem by using a concurrent
primitive at top level instead of the serial printer.
For example, suppose we have a primitive pcoerce (see chapter
6) that schedules its argument suspensions in parallel
and returns after they have all converged.
We could apply it to our top-level quicksort like so:
This would cause the suspension for quick:hi to be coerced
as well as quick:lo.
This example works because our result is not bushy;
if it were, pcoerce would likely only coerce the top-level
elements down to their first suspended cons, at which point they
would have satisfied the top-level convergance requirements of
pcoerce.
This is the problem referred to by item no. 2 above;
the suspending cons ``cuts off'' even our explicit attempt to be
parallel.
The problem with this approach is that it is naive system-level speculative parallelism (see section 2.3). There is not enough useful context information for intelligent scheduling choices. Does the entire coefficient of the running process get transferred to the first suspension created? If only part of it, how much, and to which created suspensions? The former policy would essentially default the system to an inefficient form of strictness; every suspension would be immediately scheduled after creation and the creating process would be suspended. The latter case results in massively speculative parallelism; all suspensions are scheduled with a little bit of energy. This is far too general, and undermines the purpose of laziness. Suppose the demand is for a particular element (say the 10th) of the result of our quicksort. Under this ``shotgun'' approach we expend effort across the entire structure even through the exhaustive demand in this case is ``lateral'' and then ``down''.
The limitation of the demand coefficient approach is that while it can indicate the relative overall demand for a suspension's result, it does not provide specific information about how to distribute that demand through probes or suspension creations. If the demand coefficient was not just a number, but instead a bushy list structure containing numbers, it might be a start towards conveying the demand information we need, but such a structure would be expensive to update externally, and would require more effort to interpret by the kernel. For these reasons it seems preferable to avoid general system-level speculation on new suspensions and relegate scheduling decisions to the language level (except for demand-driven scheduling).
Strictness analysis can also indicate instances where the system can be safely eager, but this bypasses some parallel opportunities where the system is being properly lazy. For example, strictness analysis does not increase parallelism in our quicksort program above, since append is not strict in its second argument. The language, being properly lazy, will suspend the recursive quicksort calls; the system, being properly demand-driven, will not schedule them until they are probed.
Consider our example;
suppose we annotate the recursive calls to quicksort like so:
Here, the @ annotation could suggest suspensions that should
be allocated remotely, thus insuring that important computations are
offloaded.
This kind of annotation might be most effective if coupled with a policy
of allocating all non-annotated suspensions locally.
We might address the second problem, inefficient demand-driven,
computation, by annotation as well.
Suppose we used the following definition of append:
Here, the $ annotations would force the recursive call to append
to be performed before returning, but still leaves append non-strict
in its second argument.
Thus, it seems that we would like both an ``important parallelism'' annotation and a demand or strictness annotation. With this in mind, I suggest three kinds of annotations: