Representing relations

Symbolic and connectionist theories seem at loggerheads throughout much of cognition, but in the domain of theories of relations, they are remarkably similar. Both classes of theories start with the same founding premise: Objects are prior to relations and atomic in the definition of relations. This makes sense: after all, ABOVE means two objects in a particular relation, one to the other. To make sense of the idea of ABOVE one has to already have the idea of OBJECT. The starting problem, then, for all classes of relational theories has been how to represent the connection between related objects that specifies the relation. Two components have been taken as critical to these representations: (1) an element that characterizes the content and arity of the relation -- that it is ABOVENESS for example and not BETWEENNESS that is being represented, and (2) a set of bindings that map the object arguments onto roles in the relation [Halford, Wilson PhillipsHalford forthcoming]. The binding of objects to roles is crucial in order to conceptually keep separate distinct situations, for example, BOOK ABOVE TABLE and TABLE ABOVE BOOK.

A brief consideration of the kinds of solutions offered to the binding problem suffices to make clear the uniformity of solutions to this representational problem. We begin with Figure 1, which offers a symbolic representation of ABOVE in which the relation term is represented by an explicit symbol, that is, the sequence of characters A, B, O, V, E. Binding is implemented by assigning particular positions in the representation to the roles of the relation and then by inserting representations of objects into these positions. This is the approach used in standard predicate-calculus notation: Above (Book, Table).

  

Figure 1: A relation represented using symbolic argument-style representation. The relation term and the arguments are symbols, the bindings are represented by the positions of the arguments.

Halford et al halfordetal:94 have proposed a connectionist version of the same kind of representation. We illustrate this in Figure 2: The relation term and the related objects are all activation vectors. They are fed into separate banks of units, places in the network, each of which is dedicated to representing a particular component. The tensor product of these three vectors (for a binary relation) is computed to complete the binding process.

  

Figure 2: A relation represented using a connectionist argument-style representation. The arguments are fed to dedicated banks of units, and their bindings are represented using the tensor product.

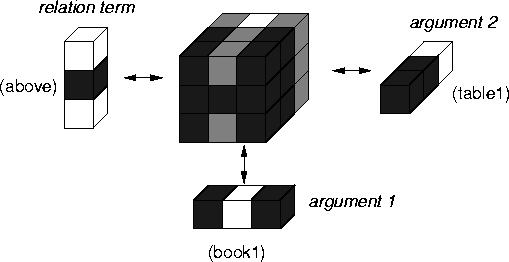Another solution to the binding problem involves pairing the objects with explicitly labeled role names (slots) rather than with places. A symbolic version of a slot-filler representation is illustrated in Figure 3. Here objects and roles are paired by concatenating the role-name symbol and the object symbol. One connectionist version of a slot-filler representation has been offered by Smolensky smolensky:90. For each role-filler pair, a role-name vector and an object vector are fed into banks of role and filler units respectively and the tensor product of these vectors is calculated. Note that the relation term may be left out if it is completely specified by the role names; e.g., in place of ABOVE we have ABOVE-HIGHER and ABOVE-LOWER. This approach is illustrated in Figure 4.

  

Figure 3: A relation represented using the symbolic explicit role representation. The binding is achieving by concatenating the role-name symbol and the filler object symbol.

  

Figure 4: A relation represented using a distributed connectionist explicit role representation. The binding of a role and its filler is computed using the tensor product or convolution.

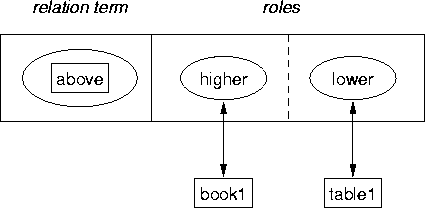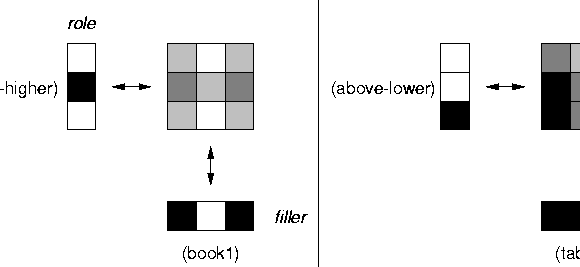In other connectionist approaches, separate role and filler units are somehow marked as belonging together rather than being placed on special purpose banks of units. In this approach, each unit in the network has an associated value (as well as an activation). When this value matches the value of another unit, they are bound together. In the dynamic binding approach [Hummel BiedermanHummel Biederman1992,Hummel HolyoakHummel Holyoak1997,Shastri AjjanagaddeShastri Ajjanagadde1993,Sporns, Gally, Reeke EdelmanSporns 1989], units ``fire'' at particular times, and units whose firings are synchronized are considered bound. This localist approach is illustrated in Figure 5.

  

Figure 5: A relation represented using a localist connectionist explicit role representation. Binding is achieved through a value that is shared by the bound role and filler (arrows in the figure).

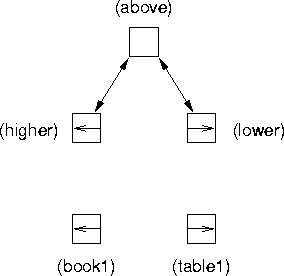Even if not reducible one to the other, all of these ways of representing relations comprise a highly similar class. Table 1 summarizes the various approaches. All assume that the specification of how the objects in a relation are related is by explicitly labeling them as being in that relation. But where does this labeling come from? How do labeled representations interface with perception and actions on objects such that the experience of a particular book and particular table manages to engage the BOOK ABOVE TABLE representation? In all of the proposals about relational representation, the relations are just there, presumed a priori abstractions. This might be acceptable if there were a universal set of innate relations hardwired some way into biology. But the developmental and cross-language evidence on this point is clear: relations are learned. Their course of development is protracted and highly influenced by language learning.

  

Table 1: Approaches to the representation of relational knowledge.

		Relation term	Bindings
	Predicate calculus	Symbol	Symbols in argument positions
Symbolic	Slot-filler	Symbol	Role symbol + filler symbol
	Argument style	Vector	Tensor product of relation and filler vectors
Connectionist	Distributed, explicit role	(Implicit in bindings)	Sum of tensor product of role and filler vectors
	Localist	Unit	Role and filler units, synchronized