►C211/  H211:   Introduction to Computer Science
▼Problem sets
►Problem set 11:   Generative recursion
On this page:
1 Generating brackets
2 Generating fractals
3 Challenge
8.14
    contents    up   

Problem set 11: Generative recursion🔗

This assignment is due on Wednesday, November 20 at 11:59pm. Submit it using Handin as assignment ps11. Corrections can be presented until Friday, December 13.

This problem set builds on the skills that we introduced in Lectures 2−9, 11−19 and 23−25. To encourage you to review those lectures, your grade on this assignment will be capped by your grade on those lectures. You can resubmit lecture exercises at any time.

Remember to follow (and when necessary, adapt) the design recipe for each function. In particular, every type mentioned in a signature must be introduced by a data definition, except for these well-known types: Number, Image, String, Color, Boolean, KeyEvent, MouseEvent, Posn, Anything, NaturalNumber, ListOfNumbers, 1String, [ListOf X], [NEListOf X]. When you write a generative recursive function, you must provide a termination argument. A termination argument must explain why the function eventually stops; it is not enough to say only when the function stops.

1 Generating brackets🔗

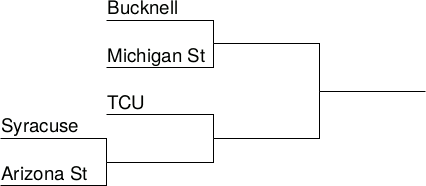
In many games (such as basketball, baseball, and euchre), two teams play against each other to see which team wins and which team loses. A tournament for such a game is a competition where many teams play against each other many times until a single team is declared the champion. Before a tournament begins, we usually make a plan that specifies which team plays against which other team at each game. Then, immediately after each game happens, it is common to eliminate the team that lost, so the loser does not play any more games and can no longer be the champion. The winner stays in the tournament and plays more games according to the plan. Eventually, a single team remains that has never lost, and that team is the champion.

Such a plan is called a bracket. In this section, you will design functions to generate a bracket before the tournament and to determine the champion after the tournament.

The following data and structure definitions represent a bracket:
; A Bracket is one of:
; - Team
; - (make-bracket Bracket Bracket)
(define-struct bracket [left right])
 
; A Team is String
For example, below are three brackets:
(define bracket1 (make-bracket "Bucknell" "Michigan St"))
(define bracket2 (make-bracket "TCU" (make-bracket "Syracuse"
                                                   "Arizona St")))
(define bracket3 (make-bracket bracket1 bracket2))

In bracket1, Bucknell plays against Michigan St. In bracket2, Syracuse plays against Arizona St, and TCU plays against the winner. In bracket3, the winner of bracket1 plays against the overall winner of bracket2 to determine the final champion.

Given a non-empty list of Teams, we want to generate a Bracket. For example, we might be given this list:
(define teams3
  (list "Arizona St" "Michigan St" "TCU" "Bucknell" "Syracuse"))
Given teams3, we want to generate bracket3. If there are two or more teams, then we need to decompose the list into two shorter lists. Let’s count off the teams by twos. In other words, let’s put teams that are adjacent in the list into different brackets. For example, in teams3, the odd elements "Michigan St" and "Bucknell" would go into bracket1, and the even elements "Arizona St", "TCU", and "Syracuse" would go into bracket2.
(define teams1 (list "Michigan St" "Bucknell"))
(define teams2 (list "Arizona St" "TCU" "Syracuse"))

Exercise 1. Design two mutually recursive functions odds and evens to decompose a list into two shorter lists. In the examples below, note that "Arizona St" goes into teams2 rather than teams1, because it is element 0 of teams3:
(check-expect (odds  teams3) teams1)
(check-expect (odds  empty ) empty )
(check-expect (evens teams3) teams2)
(check-expect (evens empty ) empty )
Similarly, the odd elements of (list "a" "b" "c" "d") are "b" (element 1) and "d" (element 3):
(check-expect (odds  (list "a" "b" "c" "d")) (list "b" "d"))
(check-expect (evens (list "a" "b" "c" "d")) (list "a" "c"))
Hint: Follow the template for processing a list, but mutual recursion means that odds should call evens and evens should call odds.

Exercise 2. Design a function generate-bracket that takes a non-empty list of Teams and generates a Bracket. Decompose the problem using the helper functions odds and evens. Remember to provide a termination argument.
(check-expect (generate-bracket teams3) bracket3)

Exercise 3. After a tournament that follows a bracket plan, the outcome is represented by the following data and structure definitions:
; An Outcome is one of:
; - Team
; - (make-outcome Outcome Winner Outcome)
(define-struct outcome [left winner right])
 
; A Winner is one of:
; - "left"
; - "right"
For example, a tournament that follows bracket3 might have the Outcome below:
(define outcome3
  (make-outcome (make-outcome "Bucknell"
                              "left"
                              "Michigan St")
                "right"
                (make-outcome "TCU"
                              "left"
                              (make-outcome "Syracuse"
                                            "left"
                                            "Arizona St"))))
Design a function champion that takes an Outcome and computes the champion Team. In outcome3 for example, the Winner "right" means that "TCU" won against "Bucknell" and is the final champion.

Hint: Follow the template for processing an Outcome.

Exercise 4. To simulate how the games in a tournament might turn out, design a function fake-outcome that takes a Bracket and produces a corresponding Outcome in which the team with the shorter name always wins. If two teams playing against each other have names that are equally long, then it doesn’t matter which team wins.
(check-expect (fake-outcome bracket3) outcome3)
Hint: Follow the template for processing a Bracket. Also, use champion and string-length.

2 Generating fractals🔗

In this section, you will use the new version of draw-trip you wrote in Lab 11: Forking turtles to make pictures that contain very fine detail. You will use generative recursion to decompose the problem of generating a big picture into the problems of generating smaller parts of the picture. Here are the data definitions again:
; A Trip is [ListOf Step]
 
; A Step is one of:
; - (make-draw Number)
; - (make-turn Number)
; - (make-fork Trip)
; *Interpretation*: angle is how many degrees to turn left (counterclockwise)
(define-struct draw [distance])
(define-struct turn [angle])
(define-struct fork [child])
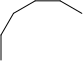
To complete this section, you don’t need to have done Lab 11: Forking turtles, but it is more fun because it lets you see the pictures you make.

Exercise 5. Recall that the repeat function in Lab 8: Turtle graphics can be used to make the following Trip. It looks like an arc, because it always draws and turns by the same amounts.
(check-expect
 (repeat 5 (list (make-draw 25) (make-turn -30)))
 (list (make-draw 25) (make-turn -30)
       (make-draw 25) (make-turn -30)
       (make-draw 25) (make-turn -30)
       (make-draw 25) (make-turn -30)
       (make-draw 25) (make-turn -30)))
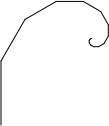Now let’s make a curlier arc—a spiral—by making each draw-distance shorter than the last. We won’t need the repeat count anymore, because we can stop when the draw-distance becomes too short (say, shorter than 1 pixel). In other words, we can decompose the problem of generating a spiral into the problem of generating a shorter and shorter spiral, until we reach the trivial problem (base case) of generating a spiral shorter than 1 pixel.

Design a function generate-spiral that takes a Number as input and generates a Trip that alternates between drawing and turning. The given number should be used as the draw-distance at the beginning of the generated Trip. Each subsequent draw-distance should be 75% of the last, but all turn-angles should still be −30 degrees. The final Step should draw with a distance shorter than 1 pixel. Below are two examples:
(check-expect
 (generate-spiral 64)
 (list (make-draw 64)                        (make-turn -30)
       (make-draw 48)                        (make-turn -30)
       (make-draw 36)                        (make-turn -30)
       (make-draw 27)                        (make-turn -30)
       (make-draw 20.25)                     (make-turn -30)
       (make-draw 15.1875)                   (make-turn -30)
       (make-draw 11.390625)                 (make-turn -30)
       (make-draw  8.54296875)               (make-turn -30)
       (make-draw  6.4072265625)             (make-turn -30)
       (make-draw  4.805419921875)           (make-turn -30)
       (make-draw  3.60406494140625)         (make-turn -30)
       (make-draw  2.7030487060546875)       (make-turn -30)
       (make-draw  2.027286529541015625)     (make-turn -30)
       (make-draw  1.52046489715576171875)   (make-turn -30)
       (make-draw  1.1403486728668212890625) (make-turn -30)
       (make-draw  0.855261504650115966796875)))
(check-expect
 (generate-spiral 0.6)
 (list (make-draw  0.6)))
Remember to provide a termination argument.

Exercise 6. Design a function generate-koch that takes a Number as input and generates a Koch curve. A Koch curve is a Trip that overall causes the turtle to move forward by the given distance. If the given distance is shorter than 1 pixel, then carry out this movement simply by make-draw. Otherwise, decompose the problem of generating a big Koch curve into the problem of generating a Koch curve that is 1/3 as big. As the example below shows, a big Koch curve is made of

  • a 1/3-as-big Koch curve,

  • a 60-degree left turn,

  • a 1/3-as-big Koch curve,

  • a 120-degree right turn,

  • a 1/3-as-big Koch curve,

  • a 60-degree left turn, and

  • a 1/3-as-big Koch curve.

(check-expect
 (generate-koch 0.6)
 (list (make-draw 0.6)))
(check-expect
 (generate-koch 1.8)
 (list (make-draw 0.6) (make-turn 60)
       (make-draw 0.6) (make-turn -120)
       (make-draw 0.6) (make-turn 60)
       (make-draw 0.6)))
(check-expect
 (generate-koch 5.4)
 (list (make-draw 0.6) (make-turn 60)
       (make-draw 0.6) (make-turn -120)
       (make-draw 0.6) (make-turn 60)
       (make-draw 0.6)                  (make-turn 60)
       (make-draw 0.6) (make-turn 60)
       (make-draw 0.6) (make-turn -120)
       (make-draw 0.6) (make-turn 60)
       (make-draw 0.6)                  (make-turn -120)
       (make-draw 0.6) (make-turn 60)
       (make-draw 0.6) (make-turn -120)
       (make-draw 0.6) (make-turn 60)
       (make-draw 0.6)                  (make-turn 60)
       (make-draw 0.6) (make-turn 60)
       (make-draw 0.6) (make-turn -120)
       (make-draw 0.6) (make-turn 60)
       (make-draw 0.6)))
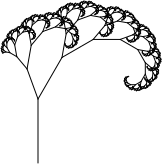Remember to provide a termination argument.

Exercise 7. Design a function generate-tree that takes a Number as input and generates a Trip just like generate-spiral does, but adds a fork before each turn. The child turtle in the fork should turn left 20 degrees (not turn right 30 degrees) then make a sub-tree that is 50% as big (not 75% as big) as the overall tree.
(check-expect
 (generate-tree 2)
 (list (make-draw 2)
       (make-fork (list (make-turn 20)
                        (make-draw 1)
                        (make-fork (list (make-turn 20)
                                         (make-draw 0.5)))
                        (make-turn -30)
                        (make-draw 0.75)))
       (make-turn -30)
       (make-draw 1.5)
       (make-fork (list (make-turn 20) (make-draw 0.75)))
       (make-turn -30)
       (make-draw 1.125)
       (make-fork (list (make-turn 20) (make-draw 0.5625)))
       (make-turn -30)
       (make-draw 0.84375)))
(check-expect
 (generate-tree 1)
 (list (make-draw 1)
       (make-fork (list (make-turn 20)
                        (make-draw 0.5)))
       (make-turn -30)
       (make-draw 0.75)))
(check-expect
 (generate-tree 0.6)
 (list (make-draw 0.6)))
Remember to provide a termination argument.

3 Challenge🔗

Make a function that generates this fractal:

Hint: Design two mutually recursive functions, one that generates all the images on the left below, and another that generates all the images on the right below. We’ve colored the lines drawn by the first function in red and by the second function in blue, but you don’t need to do that.

    contents    up