In this section we show how Contrastive Hebbian Learning (CHL)
[Movellan, 1990] needs
to be modified to accommodate units with relative phase angles.
We follow the derivation in Movellan closely.
Movellan defines a continuous Hopfield Energy function
where E reflects the constraints imposed by the weights in the network and S the tendency to drive the activations to a resting value. For our network S is the same as for a network with no phase angles:
where n is the number of units in the network, 
is
the activation of unit i, 
is the
activation function for unit i, and 
.
However, E becomes
where 
is the weight connecting
units i and j and
is the coupling function associated with units i and
j.
In what follows we will abbreviate 
as 
.
The coupling function must be differentiable and satisfy the following:
When the network is stable, the inverse of the activation function for each unit is equal to the input into that unit:
where ( 
) represents equilibrium and 
is the input
to unit i.
Furthermore, when the network is stable, the phase angle of each unit
no longer changes:
Movellan defines the contrastive function J as
and shows that the CHL rule minimizes J. We follow his derivation for the case where units have phase angles.
The energy of the network E at equilibrium is
Extracting the terms with a term,
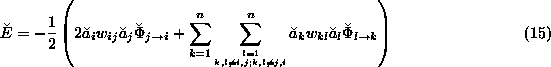
Differentiating with respect to a single weight and
considering that is the only weight depending on ,
From Equation 10, we have
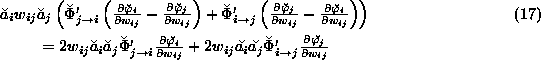
and
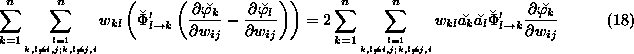
Substituting these into Equation 16,
From 11 and 12, we have the
following for the case where 
. Since there are no
self-recurrent connections in our network, we need only consider this
case.
From 12, the last term is 0, and we have
From Equation 7,
and from Equation 11, we have
making
which shows that the modified CHL rule
descends in the J function.
