Changing from the rank-1 update version of LU factorization to a matrix-vector version was done to get a better BLAS-2 kernel (in terms of load/store analysis) as the workhorse. But since the best BLAS kernel is matrix-matrix multiplication, we should try to get a BLAS-3 version. This can be done by blocking.
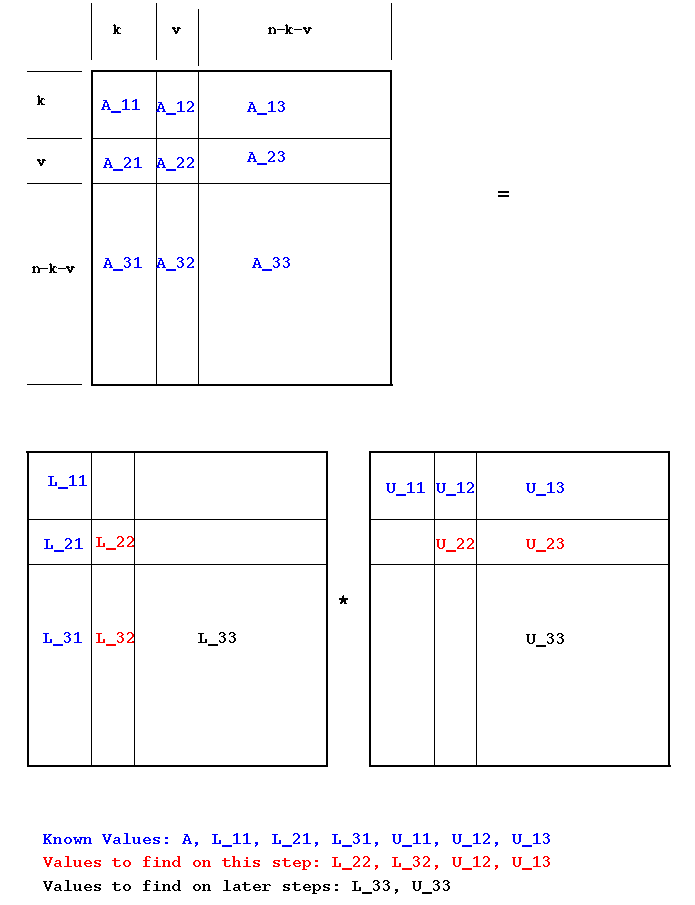
Block versions of LU factorization are derived in the same way as was done to get the matrix-vector product version. Partition the matrix into block columns, each of width v. We can find v columns of L and v rows of U on each "iteration". Suppose that k columns/rows have already been found. The picture is

where the unknowns are shown in red and the known values in blue. This is the same as the last diagram, but with block columns replacing the unknown row/column to find at this step. In more detail showing the sizes and shapes of the systems,
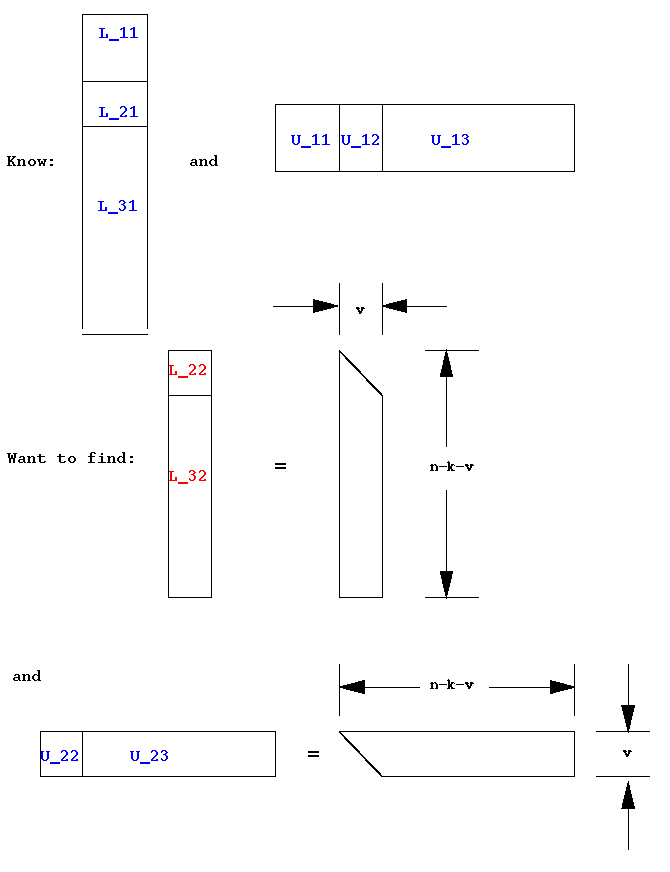
Sequencing the known/unknowns in order gives:
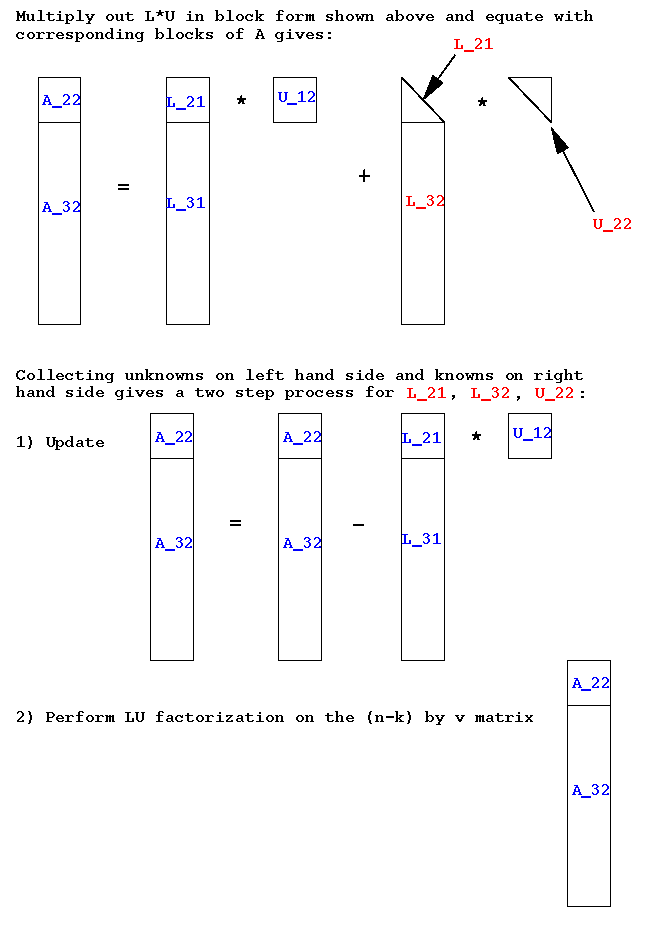

The precise algorithm statement is left as an unassigned exercise. You should implement your resulting algorithm in Matlab to verify its correctness.
The reason for using a matrix-vector product earlier was that it gave better computational kernels. However, when using a block version the rank-1 update becomes a rank-v update and so becomes matrix-matrix multiplication. That kernel is the best amongst the BLAS in terms of its ratio of memory references to flops, so we can safely use it in a high-performance version of LU factorization, instead of the version above based on the block matrix-vector version. This also makes a good review question to make sure you have understood things so far: write out the block version of the matrix*vector based decomposition.
Another point: as with the block matrix-vector (which is really a matrix-matrix version as well) shown above, the step following the scaling of subdiagonal entries consists of multiplying the following rows of the unreduced parts of A using those scaled entries. When converting it to a block version, the equivalent is to apply a lower triangular L solve on the corresponding block row, as happened above. That is indicated below by the Matlab tril(*,−1) operator returning the strictly lower triangular part of its argument. That is added to the identity matrix since L is unit lower triangular. The triangular solve is applied with overwriting to the entire block row.
Implementing this using the BLAS is relatively straightforward. Step 2 is a call to an LU factorization function with pivoting, applied to the rectangular array A(k:n,k:k+b−1). That in turn should be the matrix-vector product version of LU factorization. This is why it was stated for rectangular arrays earlier, so that it could be used as a subfunction here. Step 4 is a sequence of calls to the BLAS routine dswap() to swap rows in the columns that were not already swapped by the call to the BLAS-2 rectangular LU factorization. Step 5 is a call to dtrsm(), and step 6 is a call to dgemm().
Before diving in and trying to implement the above algorithm, first draw the corresponding block pictures as was done above for the other versions. The Matlab function LU8.m implements this, with the kludge of having to having to specify the lower triangular solves with multiple right hand sides using (eye(nub)+tril(A(cols,cols),-1)). A C or Fortran version will just call the BLAS routine dtrsm() passing along the relevant parts of the array A. The Matlab script testLU8.m will set up different arrays and call LU8.m. It uses a switch/case construct to choose what test case to create, and prompts the user for which one to select - so the script is useful as an example of how to do those things in Matlab.
The algorithms here just produce the LU factorization. A complete solver will need to also do the triangular solves (trivially done with a BLAS library: two calls to dtrsv() ). What should be done if a zero or very small pivot entry is encountered? Quit, keep going, or switch over to full pivoting? In terms of implementing a scientific computing library, the basic principle is to return to the user enough information so that person can make those difficult decisions.
The library LINPACK, and its modern successor LAPACK, separate the factorization from the solves partly to force the user to decide whether to proceed after the factorization finishes. Then the user can call the triangular solves to solve a system Ax = b for a particular right hand side vector b, or to use a different factorization if the LU one was not sufficiently accurate. Almost all good linear algebra libraries will return information like an approximation of the condition number of the matrix to help the user decide what to do next.
The real goal here is the process of using load-store analysis, and moving from an abysmal vector update or rank-1 update version to a nifty BLAS-3 matrix-matrix one. The important feature is being able to use load/store analysis to know if and when a better implementation exists, and to know how to achieve those better performing versions. More generally: