Gaussian Elimination (LU Factorization) and the BLAS

Gaussian Elimination

The most commonly used direct method for solving general linear systems is Gaussian elimination with partial pivoting, which in modern terms is called LU decomposition with pivoting, or LU factorization with pivoting. You probably learned Gaussian elimination by adjoining the right hand side vector b to the matrix, then performing row combinations that would zero out the subdiagonal entries of the matrix A. LU decomposition (or "LU factorization") does the same operations, but ignores the right hand side vector until after the matrix has been processed. In particular: Let A be an n x n nonsingular matrix. Gaussian elimination with partial pivoting gives the factorization P*A = L*U, where

The linear system Ax = b then is equivalent to LUx = Pb, since PAx = Pb. Given the factors P, L, and U, solving LUx = Pb has three steps:

  1. Set d = Pb, either by shuffling entries of b, or by accessing via indirect addressing using a permutation vector. In setting d = Pb, sometimes b can be overwritten with its permuted entries ... depending on how P is represented.
  2. Solve Ly = d (unit lower triangular system)
  3. Solve Ux = y (upper triangular system)
Solving a triangular system is easy. It can be implemented by overwriting the right hand side vector b with the solution, avoiding extra storage for additional vectors y and d. In that case the three steps look more parsimonious with space:
  1. Set x = Pb
  2. Solve Lx = x (unit lower triangular system)
  3. Solve Ux = x (upper triangular system)
and if the original right hand side vector b is not needed later on, x can be replaced with b in all three steps.

Warning: the n x n permutation matrix P is not stored as an n x n array. Instead it is stored as an 1-D integer array, usually called ipiv. Initially this will be ignored, and the factorization stated as A = L*U. In this case, what is the load/store analysis? The minimal number of memory references is n2 words for A, and n2 for L and U (since L is unit lower triangular, and so the ones on its main diagonal need not be stored.) That gives m = 2 n2. Later (after deriving the first version of LU factorization) it can be shown that the number of flops is f ≈ (2/3) n3. [The exact count is f = (1/6)*n*(4*n+1)*(n-1), if you want to be precise.] So the ratio of memory references to flops is r = 3/n → 0 as n → ∞. That means some implementation exists for which near peak performance of a computer should be achieved. The eventual goal is now to find that implementation.

LU Factorization, Part 1

The classical algorithm you probably learned (and may need to unlearn) follows a four phase sequence on each step: find the ""pivot"", interchange rows to bring the pivot to the diagonal position, scale the subdiagonal entries in the column, then update the rest of the matrix.

Omitting the first two steps that implement pivoting, the process zeros out the subdiagonal elements by adding a multiple of row k to rows k+1, k+2, ..., n, each step introducing a zero in the elements A(k+1,k), A(k+2,k), ..., A(n,k). After doing this for the first n-1 rows, the array A contains the upper triangular matrix U. The multipliers of row k that were added to the other rows are stored in the elements A(k+1,k), A(k+2,k), ..., A(n,k) since we know those are zeroed out. Those multipliers are the strictly lower triangular components of the unit lower triangular matrix L.

So carrying out these operations with overwriting of the array A gives the L and U factors in the corresponding parts of A (since L is unit lower triangular, its diagonal doesn't need to be explicitly stored, so everything fits tidily). Temporarily ignoring pivoting, the algorithm is:

LU Factorization: Triply Nested Loops Version 

for k = 1:n-1
  for i = k+1:n
      A(i,k) = A(i,k)/A(k,k)
  end for
  for i = k+1:n
      for j = k+1:n
        A(i,j) = A(i,j) - A(i,k)* A(k,j)
      end for 
  end for
end for
A Matlab function for this is in LU1.m, but it uses different index variables (r, c, i) instead of the (k, i, j) shown above. Notice that the innermost loop (on j) implements a vector update or daxpy() operation. That makes sense; the algorithm was derived by adding a multiple of one row to another, which is vector update where the vectors are the rows of the array A. Load/store analysis says implementing the algorithm this way gives a ratio of r = 3/2, which is not good. In fact, although this version is the one most readily derived, it's also the one that usually has the worst performance.
Matlab notation (AKA colon notation) helps cut down the rat's nest of indices in the loops:
  1. A(r:s, i) refers to rows r through s in column i,
  2. A(r, i:j) refers to columns i through j in row r,
  3. A(r:s, i:j) refers to rows r through s in columns i through j.
(1) is a column vector, (2) is a row vector, while (3) is a 2D submatrix. Now the algorithm above can be stated more succintly as

LU Factorization: Rank-1 Update Form 

for k = 1:n-1
  A(k+1:n,k) = A(k+1:n,k)/A(k,k)
  A(k+1:n,k+1:n) = A(k+1:n,k+1:n) - A(k+1:n,k) * A(k,k+1:n)
end for
The Matlab function LU0.m implements this, along with some error checking to make sure the divisor A(k,k) is not too small, A is square, etc.

This notational change is more important than saving on writing. It helps identify what the computation kernels are by following three rules for a 2D array:

  1. If both the row and column indices have a range, the referrent is a 2D array (a submatrix)
  2. If one index has a range and the other is a singleton, the entity is a 1D array (a vector).
  3. If neither index has a range, the critter is a scalar.
So in this case, A(k+1:n,k) = A(k+1:n,k)/A(k,k) is the scaling of the column vector A(k+1:n,k) by the scalar 1/A(k,k). The second line A(k+1:n,k+1:n) = A(k+1:n,k+1:n) - A(k+1:n,k) * A(k,k+1:n) is a matrix A(k+1:n,k+1:n) minus the column vector A(k+1:n,k) times the row vector A(k,k+1:n), or a rank-1 update of a matrix.

The notation can be simplified even more in Matlab (and Fortran) using indexing vectors : 

for k = 1:n-1
    I = k+1:n
    A(I,k) = A(I,k)/A(k,k)
    A(I,I) = A(I,I) - A(I,k)* A(k,I)
end for
The Matlab function LU2.m implements this but again with a different loop index r instead of k. The Matlab version also supresses the printing of every assignment by appending a semicolon at the end of each assignment operation in the loop.
This follows a useful convention: use upper case letters for vectors used for indexing (AKA index vectors), and lower case letters for scalars used for indexing. Using block indexing vectors can sometimes obscure more than it reveals, so the first form is prefered. Both of the forms shows more clearly what the operations involved are. Each iteration is a vector scaling of the subdiagonal part of column k, followed by a rank-1 update of the trailing part of the matrix. Graphically, the LU rank-1 update form procedure is:

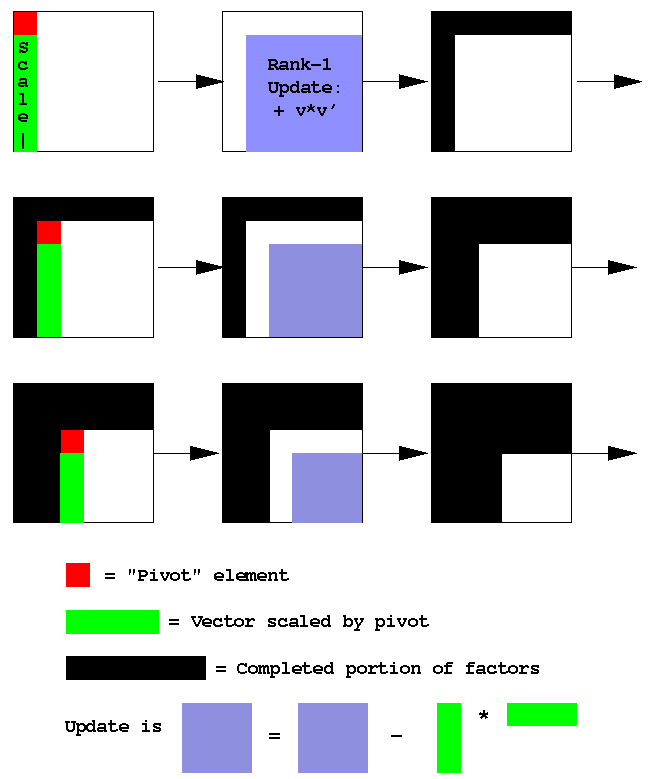
LU; Rank-1

The rank-1 update version of LU stinks as a computational kernel has a memory reference to flop ratio of 1. That is better than the 3/2 that results if it is implemented as a sequence of calls to daxpy(), but we know more efficient versions must exist.

A more efficient version comes via a common idea in computer science, where it is called "lazy evaluation". In numerical linear algebra it has a longer history, and is called "deferred updates". This means holding off application of the updating information to a part of the matrix only when it is actually needed. The algorithm results by equating parts of A, L, and U in a partitioned way. In pictures:

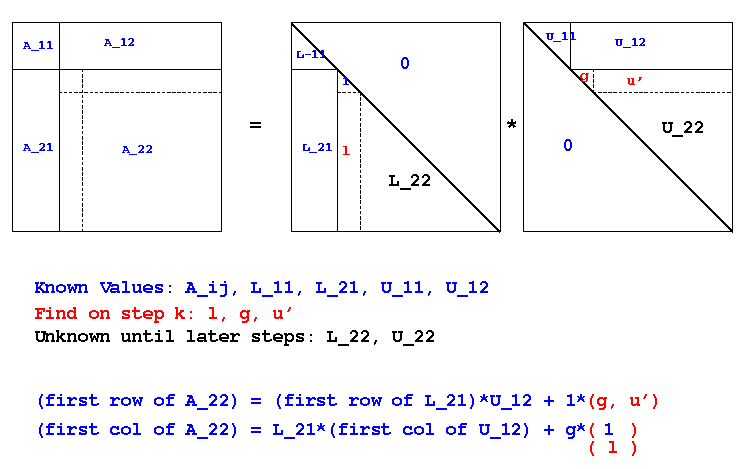
LU; Derive Mat-vec

The diagonal entry in column k of L is known to be all 1s, of course. Sequencing the finding of g, u', and l as shown above defines an algorithm which recursively works on the trailing subblock. The resulting algorithm is

LU Factorization: Matrix-Vector Product Form 

for k = 1:n-1
   A(k:n,k) = A(k:n,k) - A(k:n,1:k-1)*A(1:k-1,k)
   A(k,k+1:n) = A(k,k+1:n) - A(k,1:k-1)*A(1:k-1,k+1:n)
   A(k+1:n,k) = A(k+1:n,k)/A(k,k)
end for
In order the computational kernels in the k-loop are matrix-vector product, vector-matrix product, and vector scaling. So the rank-1 update has been replaced by matrix-vector products, which have half the memory reference to flop ratio of a rank-1 update. This is a big win on a cache-based machine. Minor point performance-wise, but big in terms of correctness: there is a final update of A(n,n) which has been left off above. Figure out what it is and correct the algorithm.

In pictures the LU matrix-vector product form procedure is:

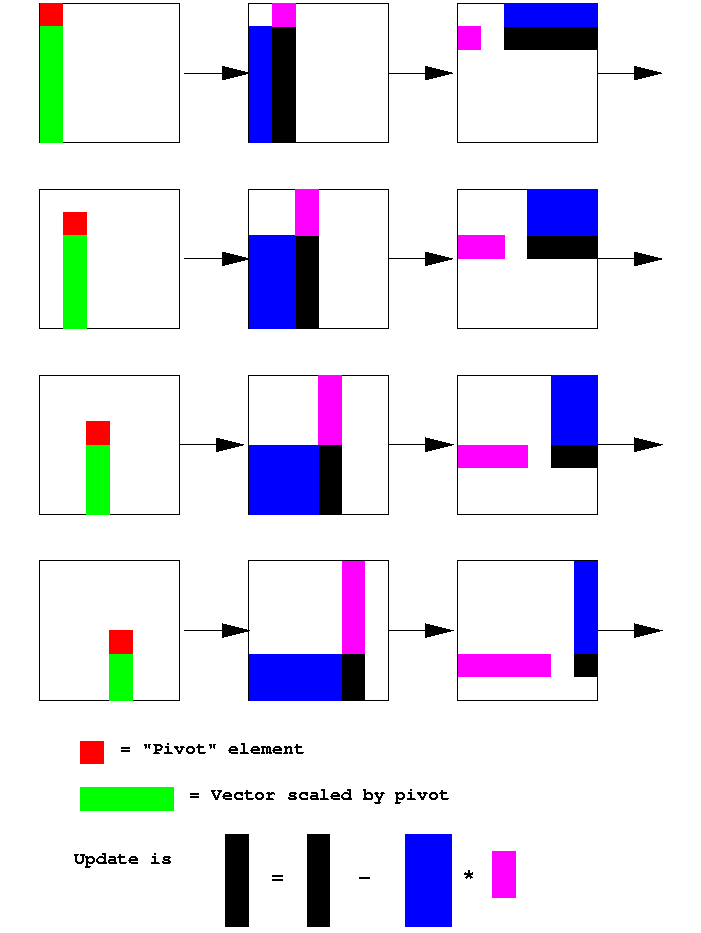
LU; Mat-vec

Three more notes:

  1. The algorithms above (rank-1 and matrix-vector product formulations) can be applied to an m × n rectangular matrix. If m > n, then L is unit lower trapezoidal and U is upper triangular. If m < n, then U is upper trapezoidal, and L is unit lower triangular.

  2. In some literature, the different versions are labeled by the order of the loops, e.g., the kij version, the jki version, etc. That requires knowing which index variable is used for which loop in the "original" version, making it harder to remember. Naming the versions based on their underlying computational kernels seems more descriptive and mnemonic, and makes shifting them to use the BLAS easier.

  3. This page has taken LU factorization from a daxpy() version (r = 3/2), to a dger() version (r = 1) to a dgemv() version (r = 1/2). The load/store analysis at the start shows a version exists with r = 0; that will be found after first dealing with the other parts of solving a linear system, permutations and triangular solves.

Next: Permutation/pivot vectors and triangular solves