1. Quaternions Describe Orientations in
3D:
Quaternions
are vectors in four-dimensional Euclidean space (R4)
and unit-quaternions represent orientations in three-dimensional
space. An orientation can be thought of as a triad of three mutually
perpendicular axes.
Quaternions are used in this manner to represent
orientations as one sweeps along a curve in 3D. Since quaternions are
four-dimensional vectors (think quaternion, q = (w, x, y, z), where w,
x, y, z ε R, real-numbers), they are visualized by projecting the
three out of the four components of each quaternion into the
three-dimensional subspace. A visualization of these quaternions is called
the quaternion-map
2. Quaternion Maps:
Quaternion maps are obtained by connecting a set of
quaternions to form a smooth curve, surface, or
volume. Quaternion curve maps can be open or
closed curves. Since the configuration of the quaternion map
signifies successive orientations of a frame in 3D space, a closed
quaternion curve indicates that the starting and end frames have the
same orientation in 3D. An open quaternion-curve may or may not
imply the same. This is because the mapping between orientations in
3D and quaternions is a 1:2 mapping, which implies that
each 3D orientation is represented by a pair of quaternions (with
opposite sign). This property is referred to as the 'double cover'. If
the end quaternions in an open quaternion-curve form such a pair, the
orientations in 3D will be identical.
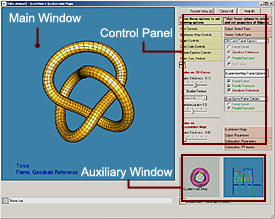
The application demonstrates orientations of frames
that sweep closed, knotted curves such as torus knots. A highly
interesting problem in itself is how the frames are assigned to a given
curve. Three framing methods are exposed in this application, namely the
Frenet-Serret, Parallel Transport, and Geodesic
Reference framings.
The figure below shows quaternion maps corresponding
to the three framing methods mentioned above:
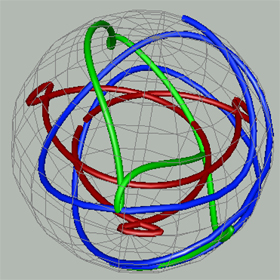
Figure 2: Quaternion Maps for: Frenet-Serret (blue),
Parallel Transport
(green) and Geodesic Reference (red).
The wire-frame sphere is the unit sphere in quaternion space.